Resumo extraído do capítulo 3 do livro Modern Control Engineering de Katsuhiko Ogata, 5ª edição

Capítulo 3 – Modelos Matemáticos para Sistemas Mecânicos e para Sistemas Elétricos

---

3–1 INTRODUÇÃO

Esta secção introduz o objectivo e o conteúdo geral do Capítulo 3, que trata da modelação matemática de sistemas mecânicos e eléctricos no contexto de engenharia de controlo.

No capítulo anterior (Capítulo 2), foram apresentados exemplos muito simples: um circuito eléctrico básico e um sistema mecânico elementar. Esses exemplos serviram para introduzir as ideias fundamentais de modelação. Agora, o propósito é generalizar e sistematizar o processo de modelação, aplicando-o a sistemas mais realistas e variados que se encontram com frequência em problemas de controlo.

O objectivo principal é mostrar como se podem obter modelos matemáticos de sistemas físicos que descrevam a sua dinâmica, ou seja, como a saída ou estado do sistema evolui em resposta a entradas ou forças actuantes. Esses modelos matemáticos podem depois ser usados para:

• Análise do comportamento dinâmico (por exemplo, estabilidade, resposta transitória).

• Projecto e síntese de controladores (compensadores, realimentação de estados).

• Simulação computacional.

Os dois domínios principais que serão estudados:

• Sistemas mecânicos, cuja dinâmica é governada pela segunda lei de Newton. Na Secção 3–2, será feita a aplicação directa dessa lei para derivar modelos de sistemas mecânicos mais complexos, incluindo a dedução de funções de transferência (que relacionam entrada e saída no domínio de Laplace) e modelos em espaço de estados (representação em termos de variáveis de estado e equações diferenciais de primeira ordem).

• Sistemas eléctricos, cujo comportamento segue as leis de Kirchhoff (lei das correntes e lei das tensões). A Secção 3–3 apresentará como aplicar estas leis a diferentes circuitos eléctricos, incluindo circuitos com resistências, bobines, condensadores e amplificadores operacionais (AmpOps), componentes muito usados em circuitos de controlo, filtros e compensadores.

---

3–2 MODELAÇÃO MATEMÁTICA DE SISTEMAS MECÂNICOS

A Secção 3–2 apresenta métodos sistemáticos para obter modelos matemáticos de sistemas mecânicos, fundamentais para o projecto e análise de sistemas de controlo. A abordagem baseia-se directamente na segunda lei de Newton, que relaciona forças com acelerações.

---

Molas em paralelo e em série

• Apresenta como determinar a constante de mola equivalente (keq) para arranjos de molas:

  • Em paralelo: as constantes somam-se directamente (keq = k₁ + k₂).

  • Em série: a constante equivalente obtém-se pela fórmula do tipo resistência em paralelo (1/keq = 1/k₁ + 1/k₂).

• O Exemplo 3–1 mostra como deduzir estas fórmulas analisando as forças e deslocamentos nos sistemas representados em figuras.

---

Amortecedores em paralelo e em série

• Um amortecedor é descrito como um amortecedor viscoso (óleo), gerando força proporcional à velocidade relativa.

• Para amortecedores:

  • Em paralelo: o coeficiente de atrito viscoso equivalente soma-se (beq = b₁ + b₂).

  • Em série: aplica-se a fórmula de resistências em paralelo (1/beq = 1/b₁ + 1/b₂).

• Exemplo 3–2 detalha estas deduções, mostrando como obter beq a partir de balanços de forças.

---

Sistema massa–mola–amortecedor montado num carro sem massa

• Analisa um sistema com uma massa m, mola de constante k e amortecedor de coeficiente b, montado num carro considerado sem massa.

• Define-se a entrada como o deslocamento do carro (u(t)) e a saída como o deslocamento da massa (y(t)).

• Aplica-se a segunda lei de Newton para escrever a equação diferencial:

  $$m \frac{d^2 y}{dt^2} + b \frac{dy}{dt} + ky = b \frac{du}{dt} + ku$$

• A transformada de Laplace (assumindo condições iniciais nulas) permite obter a função de transferência:

  $$G(s) = \frac{Y(s)}{U(s)} = \frac{bs + k}{ms^2 + bs + k}$$

• O texto explica que estas representações em função de transferência são amplamente usadas em engenharia de controlo.

• Em seguida, apresenta um modelo em espaço de estados para o mesmo sistema:

  • Define variáveis de estado.

  • Deduz as equações de estado e a equação de saída.

  • Mostra como expressar o sistema na forma matricial padrão.

---

Sistema mecânico com duas massas ligadas

• Exemplo 3–4 analisa um sistema com duas massas (m₁ e m₂) ligadas por molas e amortecedores.

• Deriva as equações diferenciais que descrevem os movimentos relativos.

• Aplica a transformada de Laplace para obter funções de transferência que relacionam entradas e saídas (forças aplicadas e deslocamentos das massas).

• Mostra como resolver sistemas de equações no domínio de Laplace para obter essas funções.

---

Pêndulo invertido montado num carro

• Exemplo 3–5 estuda um pêndulo invertido (modelo clássico em controlo), montado num carro com motor.

• O objectivo do sistema é manter o pêndulo na vertical, o que é naturalmente instável.

• Considera deslocamentos angulares pequenos para linearizar as equações:

  • Usa aproximações como sen(u) ≈ u e cos(u) ≈ 1.

• Deriva as equações de movimento usando a segunda lei de Newton para a translação e rotação.

• Obtém um modelo matemático que descreve o acoplamento entre o movimento do carro e o ângulo do pêndulo:

  $$(M + m)\ddot{x} + ml\ddot{\theta} = u$$ $$(I + ml^2)\ddot{\theta} + ml\ddot{x} = mgl\theta$$

• Estas equações descrevem a dinâmica acoplada do carro e do pêndulo.

---

Pêndulo invertido com massa concentrada no topo

• Exemplo 3–6 simplifica o modelo anterior assumindo que a massa do pêndulo está toda no topo (momento de inércia I ≈ 0).

• As equações tornam-se mais simples:

  $$(M + m)\ddot{x} + ml\ddot{\theta} = u$$ $$ml\ddot{x} + ml^2\ddot{\theta} = mgl\theta$$

• Deriva uma função de transferência do ângulo do pêndulo em relação à força de controlo aplicada ao carro.

• Mostra que o sistema tem pólos reais, um no semi-eixo positivo (indicando instabilidade em malha aberta).

• Define variáveis de estado (x, ẋ, θ, θ̇) para obter uma representação em espaço de estados completa com matriz A (dinâmica), matriz B (entrada) e matriz C (saída)

---

3–3 MODELAÇÃO MATEMÁTICA DE SISTEMAS ELÉCTRICOS

Esta secção apresenta métodos para obter modelos matemáticos de sistemas eléctricos, baseando-se nas leis fundamentais que regem os circuitos eléctricos: as leis de Kirchhoff.

Leis de Kirchhoff

• Lei das correntes (lei dos nós): a soma algébrica das correntes que entram e saem de um nó é zero.

• Lei das tensões (lei das malhas): a soma algébrica das tensões em qualquer malha fechada é zero.

Estas leis são aplicadas para escrever equações diferenciais que descrevem o comportamento de circuitos eléctricos. A partir dessas equações diferenciais, obtêm-se funções de transferência e modelos em espaço de estados.

---

Modelação de um circuito LRC

• Considere um circuito em série com indutância L, resistência R e capacitância C.

• Aplicando a lei das tensões de Kirchhoff, obtém-se uma equação diferencial que relaciona a corrente i(t) com as tensões de entrada ei(t) e saída eo(t).

• Equações diferenciais:

  $$\frac{1}{C}\int i \,dt = e_o$$ $$L\frac{di}{dt} + Ri + \frac{1}{C}\int i\,dt = e_i$$

• A transformada de Laplace (assumindo condições iniciais nulas) permite obter a função de transferência:

  $$\frac{E_o(s)}{E_i(s)} = \frac{1}{LCs^2 + RCs + 1}$$

• Também se apresenta um modelo em espaço de estados, definindo variáveis de estado adequadas para expressar o sistema como um conjunto de equações diferenciais de primeira ordem.

---

Funções de Transferência em circuitos RC em cascata com efeito de carga

• Analisa-se um sistema formado por duas malhas RC ligadas em cascata.

• Mostra-se que a ligação em cascata causa efeito de carga: o segundo circuito "carrega" o primeiro, afectando o seu comportamento.

• São deduzidas as equações diferenciais e as transformadas no domínio de Laplace, mostrando que a função de transferência global não é simplesmente o produto das funções de transferência individuais dos estágios.

• Explica-se matematicamente como surge o termo extra no denominador (representando a interacção entre os estágios).

---

Impedâncias complexas

• Introduz-se o conceito de impedância complexa no domínio de Laplace:

  • Resistor: R.

  • Indutor: LS.

  • Condensador: 1/(CS).

• As impedâncias em série somam-se, e em paralelo combinam-se como resistências equivalentes.

• Usando impedâncias complexas, pode-se obter directamente a função de transferência sem resolver as equações diferenciais originais.

• Exemplo:

  $$\frac{E_o(s)}{E_i(s)} = \frac{Z_2(s)}{Z_1(s) + Z_2(s)}$$

• Esta abordagem simplifica muito a análise de circuitos lineares.

---

Elementos em cascata sem carga

• Aborda a situação em que dois blocos são ligados em cascata sem efeito de carga (o segundo não carrega o primeiro).

• Mostra que, quando a impedância de entrada do segundo bloco é infinita (por exemplo, com um amplificador de isolamento), o modelo global é o produto directo dos modelos individuais:

  $$G(s) = G_1(s) \times G_2(s)$$

• Exemplifica a prática comum de usar amplificadores com alta impedância de entrada para evitar o efeito de carga.

---

Amplificadores operacionais (AmpOps)

• Introduz os AmpOps como componentes fundamentais em sistemas de controlo, sensores e electrónica em geral.

• Explica o funcionamento básico: amplificam a diferença de potencial entre os terminais de entrada, com ganho diferencial muito elevado.

• Características ideais:

  • Impedância de entrada infinita (não consome corrente).

  • Impedância de saída nula (pode fornecer corrente sem variação de tensão).

  • Necessidade de realimentação negativa para funcionamento estável.

---

Circuitos com AmpOps

• Amplificador inversor: ganho negativo proporcional a -R₂/R₁.

• Amplificador não inversor: ganho positivo proporcional a 1 + R₂/R₁.

• Malhas de atraso de 1ª ordem: redes RC com AmpOp geram um polo de 1ª ordem no domínio de Laplace.

• Malhas de avanço ou atraso: redes RC específicas configuradas com AmpOps permitem criar compensadores do tipo avanço ou atraso, úteis para ajustar margens de fase e estabilidade.

• Efeito de inversão de sinal: alguns circuitos têm ganho negativo. Mostra-se como se pode adicionar um inversor de sinal para corrigir isso se necessário.

---

PID com AmpOps

• Apresenta o controlador PID electrónico construído com AmpOps.

• Deduz a função de transferência geral:

  $$\frac{E_o(s)}{E_i(s)} = K_p + \frac{K_i}{s} + K_d s$$

• Mostra como definir os parâmetros proporcional (Kp), integral (Ki) e derivativo (Kd) em função das resistências e condensadores no circuito.

• Fornece fórmulas explícitas para determinar tempo integral (Ti) e tempo derivativo (Td) a partir dos componentes.

---

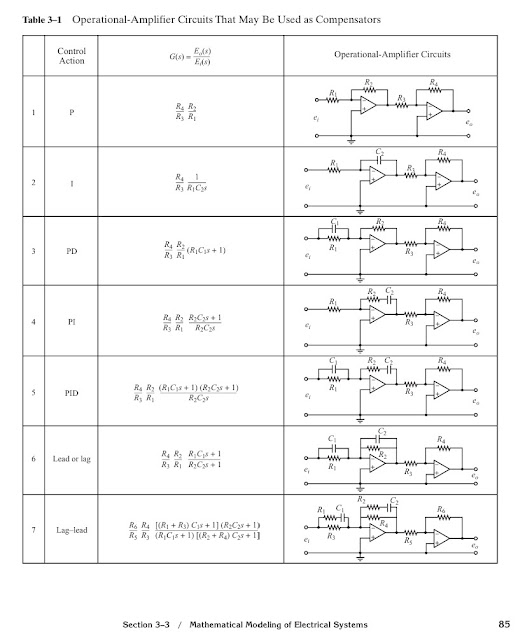
Tabela de circuitos típicos

• Inclui uma tabela (Table 3–1) com esquemas de circuitos com AmpOps usados como controladores:

  • Proporcionais (P)

  • Integrais (I)

  • Proporcionais–derivativos (PD)

  • Proporcionais–integrais (PI)

  • Proporcionais–integrais–derivativos (PID)

  • Compensadores de avanço, atraso e avanço-atraso

• Para cada configuração, mostra a função de transferência correspondente em termos dos componentes eléctricos (resistências e condensadores).

---

🎓 Quer melhorar os seus resultados na universidade? 

Disponibilizamos explicações de ensino superior adaptadas às suas necessidades, com acompanhamento personalizado para diferentes disciplinas.

✔ Explore a nossa Lista de Matérias disponíveis.

🌟 Veja os testemunhos de alunos que já atingiram melhores notas com o nosso apoio.

📬 Contacte-nos por email ou pelo formulário de contacto e obtenha a ajuda que precisa para dominar os seus estudos!

EuExplico Eu Explico Explicações de Ensino Superior

Problema de teste Controlo de Sistemas, resolvido

Resolução da Pergunta 2b do 1º teste de Controlo de Sistemas (2024-04-30), do Politécnico de Setúbal

Clique aqui para ver a resolução completa

🎓 Quer melhorar os seus resultados na universidade? 

Disponibilizamos explicações de ensino superior adaptadas às suas necessidades, com acompanhamento personalizado para diferentes disciplinas.

✔ Explore a nossa Lista de Matérias disponíveis.

🌟 Veja os testemunhos de alunos que já atingiram melhores notas com o nosso apoio.

📬 Contacte-nos por email ou pelo formulário de contacto e obtenha a ajuda que precisa para dominar os seus estudos!

EuExplico Eu Explico Explicações de Ensino Superior

Resumo extraído do capítulo 2 do livro Modern Control Engineering de Katsuhiko Ogata, 5ª edição

Capítulo 2 – Modelos Matemáticos para Sistemas de Controlo

Este capítulo foca-se em representar sistemas físicos através de funções de transferência — uma abordagem baseada na frequência e fundamental na teoria clássica de controlo. Enquanto o Capítulo 1 se centrava na modelação no domínio do tempo (com equações diferenciais), aqui passa-se para a representação no domínio da frequência, mais especificamente usando transformadas de Laplace e funções de transferência. Esta metodologia simplifica a análise de sistemas lineares invariantes no tempo (LTI), transformando equações diferenciais em equações algébricas.

O capítulo introduz a ideia de que qualquer sistema linear descrito por equações diferenciais com coeficientes constantes pode ser analisado no domínio da frequência, o que facilita o estudo da resposta do sistema a entradas variadas, a análise de estabilidade e a síntese de controladores.

---

Secção 2.1: A transformada de Laplace

Esta secção introduz e define a transformada de Laplace, que converte funções no domínio do tempo $f(t)$ em funções de variável complexa $F(s)$ no domínio da frequência. A definição da transformada de Laplace unilateral é apresentada como:

$$F(s) = \mathcal{L}[f(t)] = \int_0^\infty e^{-st} f(t) dt$$

São discutidas as propriedades fundamentais da transformada, incluindo:

• Linearidade

• Deslocamento no tempo

• Derivadas e integrais

• Teorema do valor inicial e final

A transformada é particularmente útil para resolver equações diferenciais, pois transforma a operação de diferenciação numa multiplicação algébrica por $s$, simplificando a análise de sistemas.

Além disso, a secção fornece várias transformadas comuns e usa exemplos para mostrar como aplicar a transformada de Laplace para resolver equações diferenciais ordinárias que descrevem sistemas dinâmicos.

---

Secção 2.2: Função de transferência de Sistemas Lineares

Esta secção define a função de transferência como a razão entre a transformada de Laplace da saída e da entrada de um sistema, assumindo condições iniciais nulas:

$$G(s) = \frac{Y(s)}{U(s)}$$

São analisados diferentes tipos de sistemas físicos (mecânicos e elétricos), ilustrando como derivar as suas funções de transferência a partir das equações diferenciais que os governam. Exemplos incluem:

• Sistemas massa-mola-amortecedor

• Circuitos RLC

Para cada tipo de sistema, a equação diferencial é transformada numa equação algébrica via transformada de Laplace e reorganizada para obter $G(s)$.

A função de transferência fornece uma descrição completa do comportamento dinâmico do sistema (para sistemas LTI), permitindo prever a resposta a entradas arbitrárias no domínio da frequência.

---

Secção 2.3: Diagrama de Blocos

Esta secção introduz os diagramas de blocos, uma ferramenta gráfica para representar a interligação de sistemas dinâmicos e os fluxos de sinal. Cada bloco representa um subsistema com a sua função de transferência associada, e as conexões entre blocos representam as relações de sinal (soma, subtração, ramificações).

São introduzidas várias regras fundamentais de simplificação de diagramas de blocos, tais como:

• Combinação de blocos em série e paralelo

• Realimentações (feedback)

• Movimentação de somadores e ramos

São fornecidos exemplos para mostrar como converter uma equação diferencial num diagrama de blocos equivalente, e como simplificar esse diagrama para obter a função de transferência global de sistemas compostos. Esta técnica é essencial para a modelação modular e análise de sistemas complexos de controlo.

---

Secção 2.4 – Modelação no Espaço de Estados 

Esta secção introduz a abordagem moderna à modelação de sistemas dinâmicos — a representação no espaço de estados — que se tornou essencial com o aumento da complexidade dos sistemas e o uso intensivo de computadores no projeto de controlo.

Conceitos fundamentais:

• Estado: É definido como o conjunto mínimo de variáveis necessário para descrever completamente o comportamento de um sistema dinâmico a partir de um determinado instante e entrada.

• Variáveis de estado: São os elementos do vetor de estado, escolhidos geralmente como saídas de integradores no sistema.

• Vector de estado: Um vetor que agrupa todas as variáveis de estado.

• Espaço de estados: Um espaço n-dimensional em que cada eixo representa uma variável de estado.

Equações no espaço de estados:

O comportamento de sistemas dinâmicos é descrito por:

• Equação de estado:

  $$\dot{x}(t) = f(x(t), u(t), t)$$

• Equação de saída:

  $$y(t) = g(x(t), u(t), t)$$

Nos sistemas lineares e invariantes no tempo, estas equações assumem a forma matricial:

$$\dot{x}(t) = A x(t) + B u(t)$$

• $$y(t) = C x(t) + D u(t)$$

Exemplo:

A secção inclui um exemplo prático com um sistema massa-mola-amortecedor, onde se mostra como escolher as variáveis de estado (deslocamento e velocidade) e formular as equações no espaço de estados.

Esta representação é vantajosa para sistemas com múltiplas entradas e saídas (MIMO), sistemas não lineares e para o projeto de controladores em tempo real.

---

Secção 2.5 – Representação em Espaço de Estados de Sistemas com Equações Diferenciais Escalares 

Esta secção mostra como converter uma equação diferencial escalar de ordem n numa forma de primeira ordem no espaço de estados. Isto é essencial porque os métodos modernos de análise e controlo operam sobre sistemas de primeira ordem em forma matricial.

Casos abordados:

1. Sem derivadas da entrada (u):
   Uma equação diferencial como

   $$y^{(n)} + a_1 y^{(n-1)} + \cdots + a_n y = u(t)$$

   pode ser convertida definindo variáveis de estado sucessivas como

   $$x_1 = y, \quad x_2 = \dot{y}, \quad \dots, \quad x_n = y^{(n-1)}$$

   resultando numa forma padrão:

   $$\dot{x} = A x + B u, \quad y = C x$$

2. Com derivadas da entrada (u):
   Quando a entrada também aparece com derivadas, como:

   $$y^{(n)} + \cdots = b_0 u^{(n)} + b_1 u^{(n-1)} + \cdots$$

   O truque está em escolher variáveis de estado que absorvam as derivadas da entrada, garantindo que a equação de estado não as contenha explicitamente. A matriz B será ajustada com base nos coeficientes $b_i$, calculados a partir de uma fórmula que os reexprime em função das constantes $a_i$ e $b_i$.

Este processo é fundamental para gerar modelos equivalentes que podem ser manipulados com ferramentas modernas (como MATLAB).

---

Secção 2.6 – Transformação de Modelos Matemáticos com MATLAB 

Esta secção apresenta as funções básicas do MATLAB usadas para converter entre funções de transferência e representações no espaço de estados, e vice-versa.

Transformar de função de transferência para espaço de estados:

• Comando:

  [A, B, C, D] = tf2ss(num, den)
  

  Onde num e den são os coeficientes do numerador e denominador da função de transferência.

• Esta transformação retorna uma forma canónica controlável por padrão, mas outras formas são possíveis com manipulações adicionais.

Transformar de espaço de estados para função de transferência:

• Comando:

  [num, den] = ss2tf(A, B, C, D)
  

  Para sistemas com múltiplas entradas, é possível indicar qual entrada usar com um argumento adicional:

  [num, den] = ss2tf(A, B, C, D, iu)
  

Exemplos:

São apresentados exemplos em MATLAB mostrando a aplicação dos comandos a sistemas simples, verificando que a conversão é consistente e mantendo a equivalência matemática entre as representações.

Esta secção destaca o poder e a utilidade das ferramentas computacionais para a análise e síntese de sistemas de controlo complexos.

---

Secção 2.7 – Linearização de Modelos Matemáticos Não Lineares 

Esta secção trata do processo de linearização, uma técnica essencial para lidar com sistemas não lineares, ao aproximar o comportamento do sistema em torno de um ponto de operação em equilíbrio.

Sistemas não lineares:

• Um sistema é considerado não linear quando não obedece ao princípio da sobreposição.

• Muitos sistemas físicos apresentam não linearidades (como saturação, zona morta, ou comportamentos quadráticos), mesmo que sejam tratados como lineares em regime limitado.

Linearização em torno de um ponto de equilíbrio:

• Na prática, os sistemas operam muitas vezes próximos de um ponto de equilíbrio (estado estacionário), o que permite aproximar o sistema por um modelo linear válido nesse intervalo.

• A técnica baseia-se no desenvolvimento em série de Taylor da função não linear em torno de um ponto de equilíbrio $(x_0, y_0)$, desprezando os termos de ordem superior:

  $$y = f(x) \approx f(x_0) + \left.\frac{df}{dx}\right|_{x_0} (x - x_0)$$

• Para sistemas com múltiplas variáveis de entrada (e.g. $x_1, x_2$), a aproximação linear torna-se:

  $$y - y_0 \approx \frac{\partial f}{\partial x_1} (x_1 - x_{10}) + \frac{\partial f}{\partial x_2} (x_2 - x_{20})$$

Aplicações:

• Esta abordagem permite aplicar as ferramentas de controlo linear a sistemas originalmente não lineares, desde que as variações em torno do ponto de equilíbrio sejam pequenas.

• Inclui-se um exemplo de linearização da equação $z = x y$, mostrando o cálculo do erro ao substituir o modelo exato pelo linearizado.

---

Secção 2.8 – Modelos de Sistemas Dinâmicos com MATLAB 

Esta secção mostra como usar o MATLAB para criar e manipular modelos de sistemas dinâmicos representados por funções de transferência e representações em espaço de estados.

Funções principais apresentadas:

1. Criação de uma função de transferência:

   sys = tf(num, den)
   

2. Criação de um sistema em espaço de estados:

   sys = ss(A, B, C, D)
   

3. Conversão de uma função de transferência para espaço de estados:

   [A, B, C, D] = tf2ss(num, den)
   

4. Conversão inversa – espaço de estados para função de transferência:

   [num, den] = ss2tf(A, B, C, D)
   

5. Impressão da função de transferência:

   printsys(num, den)
   

Exemplos práticos:

Incluem-se exemplos detalhados onde são aplicadas estas funções:

• Representações de sistemas com múltiplos blocos (em cascata, paralelo ou com realimentação).

• Verificação de equivalência entre modelos diferentes (transferência vs. espaço de estados).

• Uso de comandos series, parallel e feedback para combinar blocos.

Esta secção prepara o leitor para análises mais avançadas com auxílio computacional.

---

Secção 2.9 – Observações Finais sobre a Modelação de Sistemas 

Esta secção encerra o capítulo com reflexões importantes sobre a prática de modelação.

Pontos principais:

• Modelos matemáticos são aproximações: Um modelo é sempre uma representação simplificada da realidade. O nível de detalhe a incluir depende do objetivo da análise.

• Validade limitada: Um modelo que é válido para uma condição de operação pode não ser adequado noutras. Isso reforça a importância de:

  • Validar o modelo com dados experimentais.

  • Reconhecer a existência de propriedades negligenciadas (não linearidades, parâmetros distribuídos, atrito, etc.).

• Escolha da representação: Dependendo do tipo de análise (resposta no tempo, frequência, controlo ótimo), pode ser mais conveniente usar:

  • Funções de transferência para sistemas SISO lineares.

  • Espaço de estados para sistemas MIMO ou para controlo moderno.

• Linearização como ferramenta: Permite usar métodos lineares em sistemas originalmente não lineares, desde que haja limitação no intervalo de operação.

O autor reforça que a compreensão dos princípios de modelação e das suas limitações é essencial para a análise e o projeto eficaz de sistemas de controlo.

---

🎓 Quer melhorar os seus resultados na universidade? 

Disponibilizamos explicações de ensino superior adaptadas às suas necessidades, com acompanhamento personalizado para diferentes disciplinas.

✔ Explore a nossa Lista de Matérias disponíveis.

🌟 Veja os testemunhos de alunos que já atingiram melhores notas com o nosso apoio.

📬 Contacte-nos por email ou pelo formulário de contacto e obtenha a ajuda que precisa para dominar os seus estudos!

EuExplico Eu Explico Explicações de Ensino Superior

Resumo extraído do capítulo 1 do livro Modern Control Engineering de Katsuhiko Ogata, 5ª edição

Capítulo 1 – Introdução aos Sistemas de Controlo

1.1 Introdução

Este capítulo apresenta uma visão geral da teoria dos sistemas de controlo, abordando as teorias clássica, moderna e robusta. Explica a importância dos sistemas de controlo automático em diversas áreas da engenharia, como veículos espaciais, sistemas robóticos e processos industriais.

O livro destina-se a estudantes de engenharia e inclui materiais matemáticos complementares sobre transformadas de Laplace e análise vetorial-matricial nos apêndices.

Breve História do Desenvolvimento da Teoria de Controlo

• James Watt (século XVIII) desenvolveu o governador centrífugo para o controlo de velocidade de motores a vapor.
• Minorsky (1922) trabalhou em controladores automáticos para navios e estudou estabilidade.
• Nyquist (1932) desenvolveu um método para análise da estabilidade de sistemas em malha fechada.
• Hazen (1934) introduziu o termo servomecanismos e discutiu controladores de posição.
• Anos 1940–1950: desenvolvimento do diagrama de Bode e do método do lugar das raízes (Evans). A teoria clássica tornou-se predominante, baseada na resposta em frequência e no domínio da transformada de Laplace.
• Anos 1960–1980: a teoria moderna emergiu com o uso de variáveis de estado e análise no domínio do tempo, permitindo o controlo de sistemas mais complexos e multivariáveis.
• Anos 1980–1990: foco na teoria de controlo robusto, que considera incertezas nos modelos e utiliza métodos avançados para garantir estabilidade e desempenho.

1.2 Exemplos de Sistemas de Controlo

São apresentados vários exemplos práticos de sistemas de controlo:

• Sistema de controlo de velocidade: exemplificado pelo governador de Watt para motores, que ajusta automaticamente a quantidade de combustível para manter a velocidade desejada.
• Sistema de controlo de temperatura: um forno elétrico cuja temperatura é monitorizada e ajustada automaticamente.
• Sistemas empresariais: o controlo pode ser aplicado a processos organizacionais para otimizar desempenho e minimizar erros.
• Sistemas de controlo robusto: abordagem que considera incertezas no modelo do sistema, garantindo que o desempenho seja mantido apesar das variações.

1.3 Controlo em Malha Fechada vs. Malha Aberta

• Sistemas de controlo em malha fechada (feedback): utilizam realimentação para comparar o valor de saída com o valor desejado, ajustando a entrada para minimizar erros. Exemplo: um termostato regula a temperatura de uma sala.
• Sistemas de controlo em malha aberta: não possuem realimentação, operam com base em configurações predefinidas e não corrigem automaticamente desvios. Exemplo: uma máquina de lavar roupa que executa ciclos com tempos fixos sem medir a limpeza das roupas.

Comparação:
-> Vantagens da malha fechada: insensibilidade a perturbações, maior precisão e correção automática de erros.
-> Desvantagens: maior complexidade, custo e possível instabilidade se o feedback não for bem projetado.

1.4 Projeto e Compensação de Sistemas de Controlo

O capítulo introduz conceitos de projeto e compensação de sistemas de controlo:

• Compensação refere-se a ajustes no sistema para garantir que atenda às especificações desejadas. Pode ser feita por controladores PID, técnicas de resposta em frequência, lugar das raízes e espaço de estados.
• O primeiro passo no projeto é definir as especificações de desempenho, como tempo de resposta, estabilidade e erro em regime permanente.

1.5 Estrutura do Livro

Os capítulos seguintes tratam de modelação matemática de sistemas, resposta transitória e em regime permanente, análise de estabilidade, técnicas de compensação e métodos modernos de controlo, incluindo a teoria de controlo ótimo e robusto.

Se quiser tutoria e/ou explicações sobre matérias que encontre neste blogue, contacte-nos, de preferência por email. Este blogue destina-se à divulgação dos nossos serviços. É apenas uma pequena amostra do que sabemos e podemos fazer. Veja a Lista de Matérias já disponíveis para explicações. Leia testemunhos de antigos alunos.

Problema de teste de Controlo de Sistemas, resolvido

Resolução do Problema 1 do 1º teste de Controlo de Sistemas (2024-04-30), do Politécnico de Setúbal.

Clique aqui para ver a resolução completa

Se quiser tutoria e/ou explicações sobre matérias que encontre neste blogue, contacte-nos, de preferência por email. Este blogue destina-se à divulgação dos nossos serviços. É apenas uma pequena amostra do que sabemos e podemos fazer. Veja a Lista de Matérias já disponíveis para explicações. Leia testemunhos de antigos alunos.

Controlo de Sistemas - problema de teste resolvido

Resolução do Problema 1 do 1º teste de Controlo de Sistemas (2024-04-30), do Politécnico de Setúbal

Clique aqui para ver a resolução completa

Se quiser tutoria e/ou explicações sobre matérias que encontre neste blogue, contacte-nos, de preferência por email. Este blogue destina-se à divulgação dos nossos serviços. É apenas uma pequena amostra do que sabemos e podemos fazer. Veja a Lista de Matérias já disponíveis para explicações. Leia testemunhos de antigos alunos.

Resolução do teste de 02-04-2014, de Controlo de Sistemas, eng. Mecânica, IST

Modelo de suspensão activa

Se quiser explicações sobre matérias que encontre neste blogue, contacte-nos, de preferência por email. Este blogue destina-se à divulgação dos nossos serviços. É apenas uma pequena amostra do que sabemos e podemos fazer.

Contacte-nos:

Modelos matemáticos de sistemas dinâmicos

Modelação para Controlo

Alguns sistemas para exemplificar

Se quiser explicações sobre matérias que encontre neste blogue, contacte-nos, de preferência por email. Este blogue destina-se à divulgação dos nossos serviços. É apenas uma pequena amostra do que sabemos e podemos fazer.

Contacte-nos: 

Resolução - Fundamentos de Controlo IST

Resolução da pergunta I do Teste T1, de 3 de Novembro de 2011. 

Se quiser explicações sobre matérias que encontre neste blogue), contacte-nos, de preferência por email. Este blogue destina-se à divulgação dos nossos serviços. É apenas uma pequena amostra do que sabemos e podemos fazer.

Suspensão activa - Modelo matemático para Controlo de Sistemas

Resolução do teste de 02-04-2014, de Controlo de Sistemas, eng. Mecânica, IST
Pag. 1 da resolução:

Se quiser explicações sobre matérias que encontre neste blogue), contacte-nos, de preferência por email. Este blogue destina-se à divulgação dos nossos serviços. É apenas uma pequena amostra do que sabemos e podemos fazer.

Quadro resumo de controladores PID

Se quiser explicações sobre matérias que encontre neste blogue), contacte-nos, de preferência por email. Este blogue destina-se à divulgação dos nossos serviços. É apenas uma pequena amostra do que sabemos e podemos fazer.

Modelos matemáticos de sistemas físicos dinâmicos - 2

Pag. 2

Se quiser explicações sobre matérias que encontre neste blogue), contacte-nos, de preferência por email. Este blogue destina-se à divulgação dos nossos serviços. É apenas uma pequena amostra do que sabemos e podemos fazer.

Modelos matemáticos de sistemas físicos dinâmicos - 1

Pag. 1

Se quiser explicações sobre matérias que encontre neste blogue), contacte-nos, de preferência por email. Este blogue destina-se à divulgação dos nossos serviços. É apenas uma pequena amostra do que sabemos e podemos fazer.